Definition

When there is a large sum of tolerances ($n$>3), you will often see engineers doing a RSS (root sum squared) analysis of this tolerance stack to get a range that approximates the total sum of the size these these manufactured parts will fall into.

The definitions doe this analysis is as follows.

$d_{g} = \sum_{i=1}^{n} a_i d_i$

$t_{wc} = \sum_{i=1}^{n} \left|a_i t_i\right|$

$t_{rss} = \sqrt{\sum_{i=1}^{n} a_n^2 t_n^2}$

and

• Minimum WC Bounds = $d_g - t_{wc}$
• Maximum WC Bounds = $d_g + t_{wc}$
• Minimum RSS Bounds = $d_g - t_{rss}$
• Maximum RSS Bounds = $d_g + t_{rss}$

where

• $n$ = the number of independent variables (dimensions) in the stackup
• $d_g$ = the mean value at the dimension
• $a_i$ = sensitivity factor that defines the direction and magnitude for the ith dimension. In a one-dimensional stackup, this value is usually +1 or –1. Sometimes, in a one-dimensional stackup, this value may be +.5 or -.5 if a radius is the contributing factor for a diameter callout on a drawing.
• $d_i$ = the mean value of the ith dimension in the loop diagram.
• $t_i$ = equal bilateral tolerance of the $i$th component in the stackup.
• $t_{wc}$ = maximum expected variation (equal bilateral) using the Worst Case Model.
• $t_{rss}$ = maximum expected variation (equal bilateral) using the RSS method.

The RSS equation works for “equal $\sigma$” values. If the designer assumed that the input tolerances were ±4$\sigma$ values for the piecepart manufacturing processes, then the probability that the assembly is between ±$t_{rss}$ is 99.9937% (±4$\sigma$).

But where does RSS come from?

If we look at the Wikipedia article for adding normal distributions, we can se it defined as ^[1]

$X \sim N(\mu_X, \sigma_X^2)$

$Y \sim N(\mu_Y, \sigma_Y^2)$

$Z=X+Y,$

$Z \sim N(\mu_X + \mu_Y, \sigma_X^2 + \sigma_Y^2).$

Okay, so when two normal (aka Gaussian) distributions, X and Y, are added, the resulting mean is the sum of the two means, and the resulting variance is the sum of the two variances (variance = $\sigma^2$)

$Var(Z) = \sigma_X^2 + \sigma_Y^2$

$\sigma_Z^2 = \sigma_X^2 + \sigma_Y^2$

$9 \sigma_Z^2 = 9(\sigma_X^2 + \sigma_Y^2)$

$3\sigma_Z = \sqrt{9\sigma_X^2 + 9\sigma_Y^2}$

$3\sigma_Z = \sqrt{(3\sigma_X)^2 + (3\sigma_Y)^2}$

So if we assume the tolerance USL and LSL are ±3$\sigma$ (or any really), then the sum of the tolerances is the Root Sum Squared of all the tolerances.

$t_{Z} = \sqrt{t_X^2 + t_Y^2}$

With the following assumptions

• All input tolerances are assumed to have a normal distribution
• All of the input tolerances are assumed to have equal variances
• The resulting RSS variance is equivalent to the input variances

Example

Lets say we have a motor assembly and we want to make sure that when assembled, several critical requirements are always (or almost always) met.

• Requirement 1: The gap between the shaft and the inner bearing cap must always be greater than zero to ensure that the rotor is clamped and the bearings are preloaded.
• ...
• Requirement 6: The bottom of the bearing cap screw thread must never touch the bottom of the female thread on the shaft.
• ...

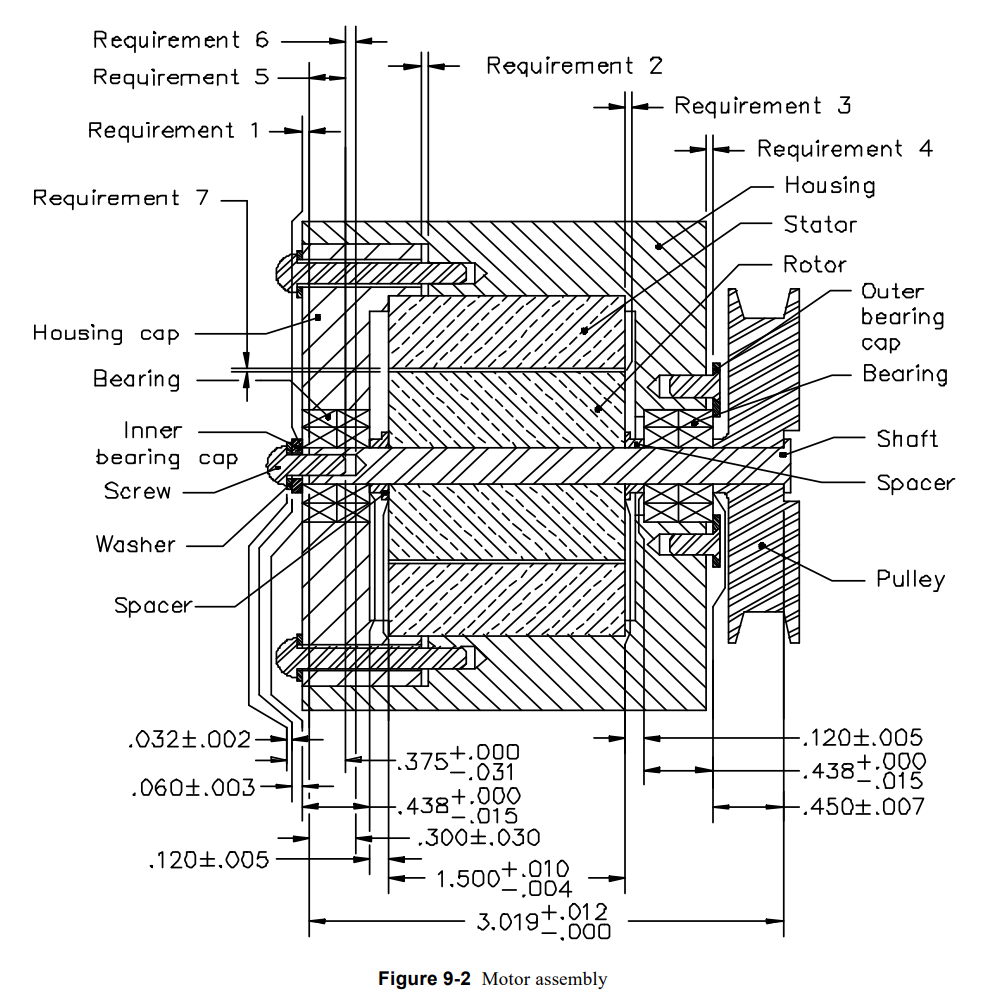
We will focus of Requirement 6 for this example. Our tolerance loop looks like this:

Stack: Motor Assembly
ID Name                     Description dir  Nom.             Tol. Sens. (a) Relative Bounds 
 6    A             Screw thread length   - 0.375   + 0 / - 0.031          1  [0.344, 0.375] 
 7    B                   Washer Length   + 0.032   ± 0.002                1   [0.03, 0.034] 
 8    C Inner bearing cap turned length   +  0.06   ± 0.003                1  [0.057, 0.063] 
 9    D                  Bearing length   + 0.438   + 0 / - 0.015          1  [0.423, 0.438] 
10    E            Spacer turned length   +  0.12   ± 0.005                1  [0.115, 0.125] 
11    F                    Rotor length   +   1.5 + 0.01 / - 0.004         1   [1.496, 1.51] 
10    G            Spacer turned length   +  0.12   ± 0.005                1  [0.115, 0.125] 
 9    H                  Bearing length   + 0.438   + 0 / - 0.015          1  [0.423, 0.438] 
12    I           Pulley casting length   +  0.45   ± 0.007                1  [0.443, 0.457] 
13    J             Shaft turned length   - 3.019   + 0.012 / + 0          1  [3.019, 3.031] 
14    K               Tapped hole depth   +   0.3   ± 0.03                 1    [0.27, 0.33]

If we so a Worst Case ans RSS analysis, these are the results.

Dimension: Motor Assembly - WC Analysis - 
ID                         Name Description dir   Nom.           Tol. Sens. (a) Relative Bounds
25 Motor Assembly - WC Analysis               + 0.0615 ± 0.0955               1 [-0.034, 0.157]
37 Motor Assembly - RSS Analysis              + 0.0615 ± 0.03808              1 [0.02342, 0.09958]

The requirement is it needed to be greater than 0. In the W.C. analysis, the bounds drop below zero, but in the RSS analysis, they do not. We can see the RSS bounds are much smaller than the Worst Case (almost 1/3 the size). If we wanted to guarantee 100% of the time, for all assemblies, the requirement is met, we would follow the WC analysis, which states the requirement will not be satisfied and we need to adjust the design, clamp down on tolerances, and pay more. If we only needed the assembly to be right ~97% of the time, we can use the RSS, and call it a day.

Demo created with: https://github.com/phcreery/dimstack

---

1. https://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables ↩︎